西南地区微电网经济调度解析:储能参与电力需求响应
发布日期:2020/2/17

储能单元在配电网的谷时电价时段进行充电,在其余时段均进行放电的运行方式,以此减少微电网从配网的购电量。
1研究背景
我国西南地区电力资源丰富,特别是在可再生能源方面有着得天独厚的优势,其风能资源、太阳能资源以及小水电资源储备丰富,有着极其广阔的开发利用前景。但受限于目前的科学技术手段,地区内新能源消纳问题较为突出,存在着大量的弃风、弃光、弃水等问题,资源浪费现象严重。微电网是分布式电源、储能系统、负荷与控制装置的集合,其通过控制装置协调各单元实现微网系统内部的发电、配电和用电,是可再生能源接入配电网的重要途径。随着微电网技术的发展,将我国西南地区的可再生能源以微电网方式运行发电,有利于缓解大电网运行压力,丰富系统电力结构,真正做到走可持续发展道路。
2论文所解决的问题及意义
微电网概念的提出既协调了分布式电源与大电网之间的矛盾,又发挥了分布式发电低能耗、供电灵活等的优点,发展前景巨大。但与此同时,微电网系统内所包含的随机性以及不确定性增加,如何进行考虑系统不确定性的微电网经济调度对电网运行单位来说是一个巨大的挑战。
本文为研究考察系统不确定性的微电网系统经济调度,首先立足西南片区实际情况建立典型并网型微电网模型,在此基础之上对微电网系统建立两阶段鲁棒优化模型,并利用Benders分解算法对所述两阶段鲁棒优化模型进行求解,以期实现对西南地区所发展的微电网系统进行经济调度研究,所做研究对西南地区微电网的进一步发展具有一定前瞻探索意义。
3论文重点内容
本文以西南某地区光伏出力以及典型城市负荷为例,考虑微电网中分布式电源和负荷的不确定性,建立基于两阶段鲁棒优化的西南地区微电网经济调度模型,引入不确定调节参数改善保守性,采用Benders分解算法来对模型进行分层求解,为含微电网的西南地区电网的调度运行提供参考策略。
(1)两阶段鲁棒优化模型的建立与求解
本文综合考虑可控分布式电源、储能单元、需求相应负荷以及微电网与配电网之间的交互成本,以微电网内各单元日运行成本最小为目标,综合考虑系统功率平衡约束、需求响应约束、分布式电源功率输出约束以及与配电网的交互功率约束等约束条件。在此基础之上,对系统中包含的光伏分布式发电单元输出功率以及负载功率的不确定性,利用盒式不确定集合进行描述,由此将问题改写为典型两阶段鲁棒优化形式。
对于上述两阶段鲁棒优化模型,本文应用Benders分解算法将模型分解为主问题和子问题进行求解。在Benders分解算法的求解过程中,子问题不断将所求解返回作为主问题的约束条件,同时,主问题也不断返回整数参数至子问题中,通过迭代,不断更新约束条件直至最优解,有效提高模型的求解效率。具体求解流程如图1所示。
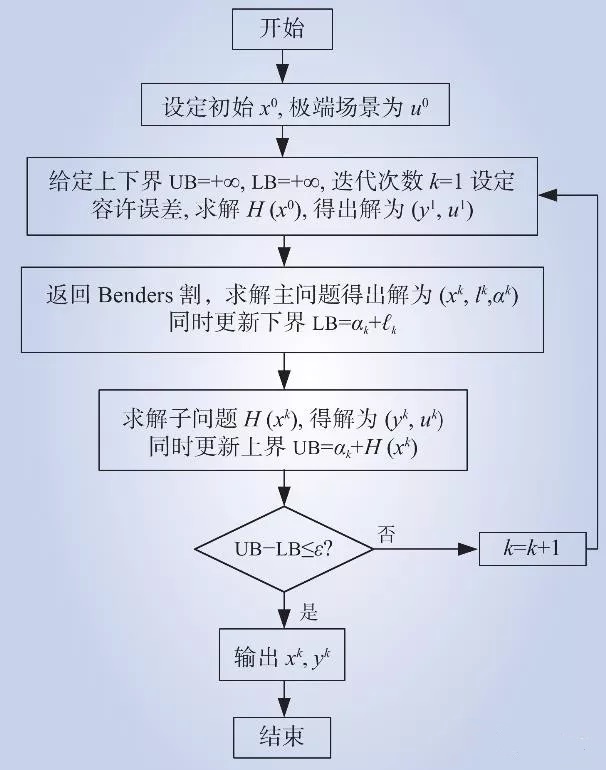
图1 Benders算法求解流程图
(2)算例分析
本文选取西南地区某地夏季典型光照与负荷数据,搭建两阶段鲁棒优化模型,采用Benders分解算法,结合Matlab和CPLEX工具箱对模型进行求解,得出考虑光伏出力和负荷不确定性的日前调度策略,为微电网接入西南电网的调度研究提供参考模型。算例所使用西南地区典型微电网结构如图2所示,可再生分布式电源为光伏电源:

图2 微电网结构图
以上述分析条件为基础,所述基于两阶段鲁棒优化的西南地区微电网经济调度研究优化结果如下:

图3所示为燃料电池输出功率以及微电网与配电网的交互功率
由图3可知,在1:00~7:00和24:00~1:00间,由于燃料电池的发电成本高于电价水平,系统运行主要依靠配网的购电,燃料电池在约束条件下以其最小功率运行。其余时段燃料电池均以最大功率运行,与储能单元、光伏电源一同将电供给负荷,减少微电网向配网的购电量,降低系统的运行成本。同时,在满足内部负荷且有富余电量的情况下,微电网在峰平电价时段(图中的7:00~18:00,20:00~21:00,23:00~24:00)售以配网,实现削谷填峰。
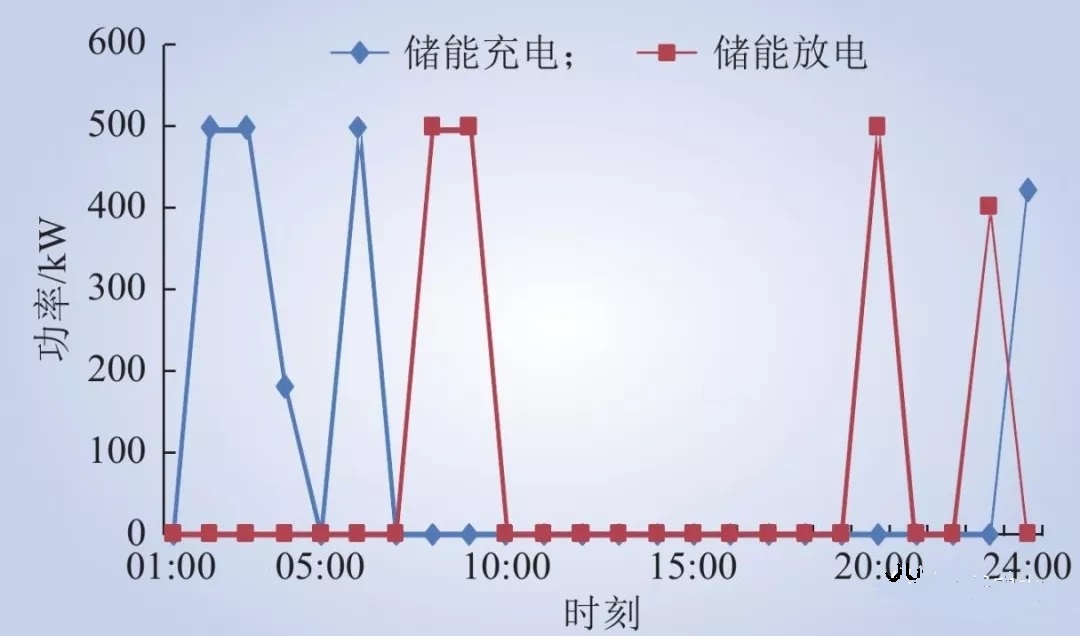
图4为储能单元的充放电功率
由图4可知,储能单元在配电网的谷时电价时段进行充电,在其余时段均进行放电的运行方式,以此减少微电网从配网的购电量。

图5为需求响应负荷实际/期望用电功率图
由图5可知,需求响应负荷的期望用电功率主要集中在峰时电价时段。经调节后,在满足相关约束条件的情况下,将用户在峰时电价时段的用电功率调节至电价低谷时期,减少了微电网在峰时电价时段的购电量,降低了微电网的购电成本。
为验证所述两阶段鲁棒优化的有效性,本文将所述两阶段鲁棒优化调度与确定性优化方案进行了进一步的分析。实际运行中,微电网需要向配网提供日前调度计划,由于预测误差的存在,实际用电量与计划用电量会有所偏差,微电网需在实时市场对差值进行补偿,而在实时运行阶段,售电价较日前电价有所降低,购电价有所升高,本文将微电网的日运行成本定义为系统日前调度成本与调整成本之和。
表1 不同优化方案下成本对比(单位:元)
从上表可以看到,虽然鲁棒优化的日调度成本高于确定性优化,但综合由预测误差带来的调整成本,最终所得鲁棒优化下的总成本较确定性优化低。以上结果说明,在进行电力系统经济调度研究时,系统内包含的不确定性将会影响到系统的经济性和安全性,而使用鲁棒优化方法,能够保证在极端“恶劣”的场景下保证系统的安全经济运行,调度结果鲁棒性强,且相对与确定性经济调度,二阶段鲁棒优化模型具有更好的经济性。
4研究结论
本文采用西南地区某市的典型光照与负荷数据,对微电网运行调度进行优化,搭建了两阶段鲁棒优化模型,结论总结如下:
(1)考虑可再生能源出力和负荷的不确定性,通过Benders分解算法实现对所搭建的模型进行求解,得出微电网在极端运行场景下的最优日前调度方案;
(2)结合实时调度的再调整成本考虑,鲁棒优化的所获总成本较确定性优化运行成本更低,表明了在进行优化调度时考虑不确定性的重要性,以及鲁棒优化在对此类问题求解方面的良好适用性。
来源:中国电力